未経験から一等無人航空機操縦士を取得するまで⑦
学科試験では数問計算問題が出題されます
CBT試験ではPC上で電卓が使えるし、計算自体はそんなに難しくないです
ただ、数回練習しておかないと単位合わせでひっかけにきた時に引っ掛かりやすいです
計算は今のところほぼ定型問題しか出ないようなので確実に取っておきたいところ
計算問題も公開されている「無人航空機の飛行の安全に関する教則」の内容から出題される
記号の名称と意味
まずは計算を行う上で基礎知識としてある程度の記号と意味を覚える必要があります
記号が被っているものもありますが、あまり気にせず
計算問題を何度か練習するうちに勝手に覚えると思います
| 記号 | 名称・意味 | 単位 | 記号 | 名称・意味 | 単位 | |
| W | 機体重量・重量 | Φ | (ファイ)バンク角・ロール角 | |||
| V(v) | 飛行速度・速度 | m/s | ω | (オメガ)回転角速度・角速度 | ||
| ρ | (ロー)空気密度・密度 | h | 高度・高さ | m | ||
| P | 仕事率・Power | g | 重力加速度 | m/s2 | ||
| D | 抗力 | L | 揚力 | |||
| d | 滑空距離・距離 | m | T | 推力 | ||
| r | 旋回半径・半径 | m | γ(ガンマ) | 滑空角・角度 | ||
| R | フレネルゾーン半径 | m | λ | (ラムダ)波長 | m | |
| D | 送受信アンテナ間距離 | m | f | 周波数 | s |
飛行機の揚力・回転翼航空機の推力
飛行機の水平飛行における関係式
W = L ∝ ρV2 機体重量 = 揚力 ∝ 空気密度・飛行速度2
プロペラなどの回転翼の推力における関係式
T ∝ ρω2 推力 ∝ 空気密度・回転角速度2
回転翼航空機(ヘリコプター・マルチコプター)のホバリング時の関係式
W = T 機体重量 = 推力
回転翼の消費パワーの関係式
P ∝ ρω3 ∝ Tω 仕事率 ∝ 空気密度・回転角速度3 ∝ 推力・回転角速度
「∝」は比例の記号です
例えば、上の式だとPが2倍になるとTωも2倍になることを表現している
例題1
回転翼航空機が440rpmの回転角速度で消費する仕事率は10Wで、この航空機が510rpmに回転角速度に上げた場合の仕事率を求める。
P ∝ ρω3 ∝ Tωの公式の P ∝ ρω3の部分を使います
まずρω3が何倍になっているのかを求めます、つまり(ρ×4603)に何倍すると(ρ×5003)になるかを考えます
5003 / 4603 = 1.284
P ∝ ρω3の右側部分は1.284倍になっていて、Pも比例するのでPも1.284倍になります
10 × 1.284 = 12.84 ≒ 13
仕事率は約13Wとなります
例題2
機体重量が10kgの回転翼航空機が、仕事率9Wで回転角速度が300rpmで飛行する機体で、ペイロード5.5kgを積載して回転角速度を400rpmに上昇させて飛行した場合の仕事率を求める
条件として空気密度は考えないものとする
P ∝ ρω3 ∝ Tωの公式の P ∝ Tωの部分を使います
まずはTωが何倍になっているかを考えるので、基本的には例題1とやり方は同じ
{(10+5.5)×400) / (10×300) = 2.067
Tωは2.067倍となっている
注意点は(10kg+5.5kg)の部分で、10kgの機体に5.5kgの物を積むから機体重量に物の重量を加算する
Tωが2.067倍になっているので、Pも2.067倍になる
9 × 2.067 = 18.603 ≒ 18.6
仕事率は18.6Wとなる
大気には標準大気が定められていて、高度と空気密度は表の通りとなる
| 高度(m) | 空気密度(kg/m3) | 高度0mとの比 |
| 0 | 1.2250 | 1.00000 |
| 500 | 1.1673 | 0.95287 |
| 1000 | 1.1116 | 0.90746 |
| 1500 | 1.0581 | 0.86373 |
| 2000 | 1.0065 | 0.82162 |
| 2500 | 0.95686 | 0.78111 |
| 3000 | 0.90912 | 0.74214 |
| 3500 | 0.86323 | 0.70468 |
例として高度3000mと0mの空気密度を比べると約0.74倍
同じ回転角速度で発生するプロペラの推力は0.74倍になる
つまり、同じ機体重量の機体を3000mの高度で飛行させるために必要な回転角速度は
√ ( 1 / 0.74 ) ≒ 1.16
となり、1.16倍の回転角速度が必要で、消費パワーも1.16倍必要となる
※「≒」はニアリーイコールといい「ほぼ等しい」という意味
飛行機の旋回半径
「飛行機がバンク角(ロール角)Φの定常旋回飛行を行うためには、力のつり合いから、水平定常飛行と比べて1 / cosΦ倍の揚力が必要」とある
V2 / r = g tanΦ 飛行速度2/旋回半径 = 重力加速度・tanΦ(バンク角)
r (旋回半径)について式を表現すると
r = V2 / g tanΦ
例題3
飛行機がバンク角30°で定常旋回飛行を行うためには、水平定常飛行と比べて必要な揚力は何倍か
条件として、sin30°=0.5 , cos30°=0.87 , tan30°=0.28とする
1/cosΦを使用して求めるので、cosΦにcos30°の値を入れる
1 / 0.87 = 1.149 ≒ 1.15
つまり1.15倍の揚力が必要となる
例題4
飛行機が飛行速度:35m/s , バンク角60°で定常旋回した時の旋回半径を求める
条件として、重力加速度:9.8m/s2 , tan60°=1.73とする
r = V2 / g tanΦを使用して求める
r(m) = 352(m/s) / (9.8(m/s2) × 1.73) ⇒(m/s) × (s2/m)
= 1225 / 16.954
= 72.254 ≒ 72(m)
旋回半径は約72mとなる
※緑の表記はわかりやすく単位を記載しているだけなので、気になれば無視で
飛行機の滑空距離
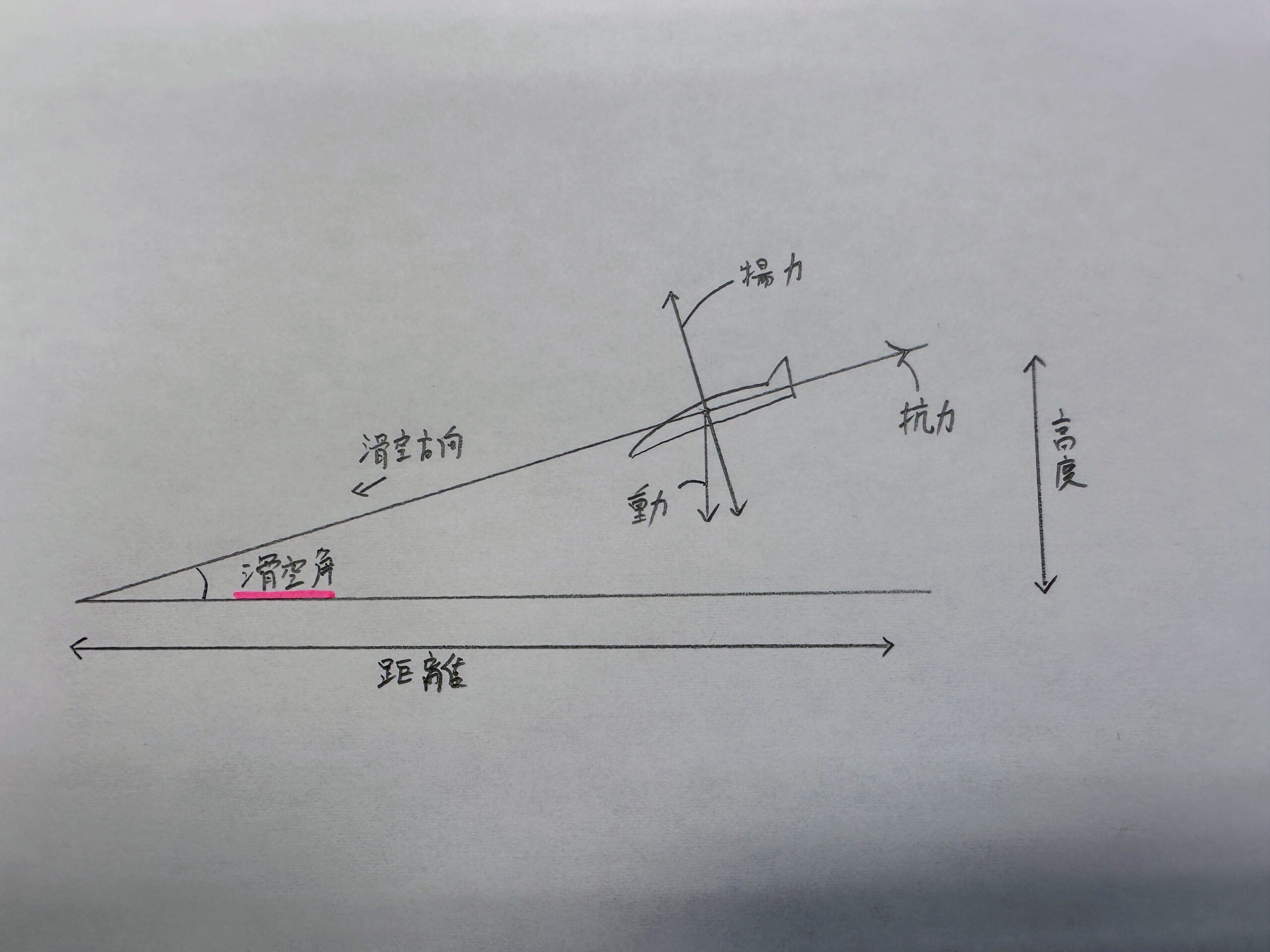
飛行機の滑空時、飛行経路が水平面となす角を滑空角(降下角)とよぶ
たぶんこんな感じ
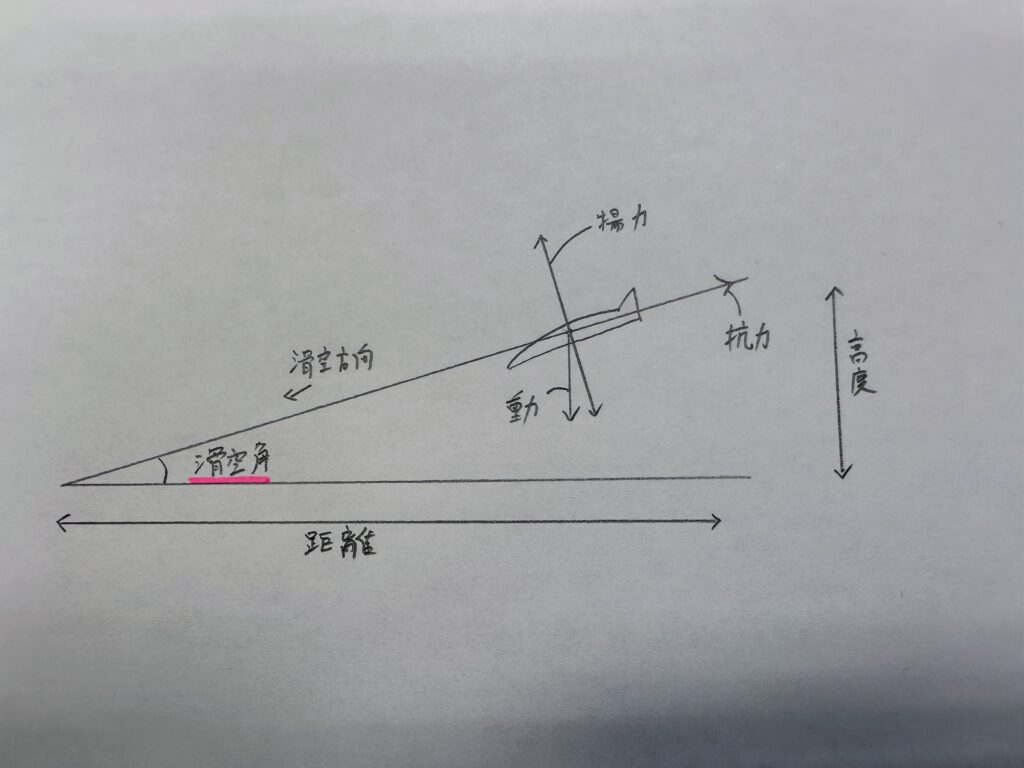
無推力の定常滑空飛行状態での滑空角γ(ガンマ)を求める式
tanγ = 1 / (L/D) tanγ(滑空角) = 1 / (揚力/抗力)
ある高度からの滑空距離を求める式
d = h / tanγ = h ・ ( L/D )
滑空距離 = 高度/tanγ(滑空角) = 高度 ・ (揚力/抗力)
L / D は揚抗比
例題5
揚抗比15、高度100mからの滑空距離を求める
d = h・(L/D)の式の対応する記号に入れるだけ
d(m) = 100(m) ・ 15 = 1500(m)
ちなみに揚抗比15の無推力の定常滑空飛行状態の滑空角γは
γ = tan-1(1/15) ≒ 3.8°
水平到達距離(水平投射の場合)
条件として、高度hを飛行する飛行速度vの無人航空機が、揚力を失い落下を始める場合で無人航空機を質点とみなせるものとし、空気抵抗は無視できると仮定
その場合の落下開始点から地上に墜落するまでの水平距離xを求める式
x = v √( 2h / g ) 水平距離=飛行速度 √(2×高度/重力加速度)
例題6
無人航空機が高度180mを飛行速度30m/sで飛行していて、揚力を失って落下を始めた場合の水平距離を求める
条件として、空気抵抗は無視できる、重力加速度は9.8m/s2とする
x = v √( 2h / g )を使用して求める
x(m) = 30(m/s) √( 2・180(m) / 9.8 (m/s2))
⇒(m/s)√{(m)×(s2/m)}⇒(m/s)√(s2)⇒(m/s)×(s)
= 30 √(36.735)
= 181.828 ≒ 182(m)
水平距離は約182mとなる
フレネルゾーン半径と必要なアンテナの高さ
フレネルゾーン半径の関係式
R = √{ λ × (D/2)2 × (1/D)}
フレネルゾーン半径=√{波長×(アンテナ間距離/2)2×(1/アンテナ間距離)}
少し計算を進めると
R = √{ λ × (D/4)}
波長λの求め方
λ = c / f 波長=光の速度/周波数
光の速度 3.0×108(m/s) は覚える
例題7
送受信アンテナ間距離が100m、使用周波数が2.4GHzの時のフレネルゾーン半径
まずは、λ=c/fを使ってλを求める
λ(m) = (3.0×108)(m/s) / (2.4×109)(s)
= 0.125(m)
GHzの「G」は10を何乗したかの指数表記で、「G=109」を意味する
これを踏まえると計算の考え方が楽になり、λを求める際の約分が楽になる
計算過程は (3.0×108) / (2.4×109) ⇒ (3.0×108) / (2.4×109)
⇒ (3.0) / (2.4×101) ⇒ 3.0 / 24 = 0.125となる
ちなみに0.125は1.25×10-1とも表現できる
次にフレネルゾーン半径をR = √{ λ × (D/4)}を使って求める
R(m) = √{ 0.125(m) × ( 100(m) / 4 )}
≒1.77(m)
フレネルゾーン半径から理想的なアンテナの高さは1.77m以上となるが、60%以上の高さが確保できていれば、フレネルゾーンに障害物がない場合と同等の通信品質を確保できるといわれている
60%の高さにするには、60/100倍 つまり0.6倍すればいいので
1.77 × 0.6 ≒ 1.06
1.06mないし1.1m以上となる
無人航空機操縦士試験のサンプル問題

これは国土交通省からで公開されている無人航空機操縦士試験のサンプル問題
定常旋回した時の旋回半径を求める問題なので、「 r = V2 / g tanΦ 」を使います
覚えた公式に与えられている数字を入れると
r(m) = 252(m2/s2) / (9.8(m/s2) × 0.58)
= 625(m2/s2) / 5.684(m/s2) ⇒(m2/s2) × (s2/m)
= 109.96 ≒ 110(m)
という計算になり答えは「b:110m」となります
計算の中での単位の動きを見てみると少しわかりやすいかもしれません
単位が邪魔であれば緑の部分を消してみてください

これはフレネルゾーン半径の60%の値を求めますので、「R = √{ λ × (D/4)}」を使います
まずλは「λ = c / f 」で求め、光の速度は「3.0×108(m/s)」です
λ(m) = (3.0×108)(m/s) / (2.4×109)(s) ⇒ (m/s) × (s/1)
= 3.0 / 24 = 0.125(m)
次にフレネルゾーン半径を求めます
R(m) = √{ 0.125(m) × (1400/4)(m)}
= √( 43.75(m2)) = 6.614(m)
最後に忘れずに60%の値を出します
6.614(m) × 0.6 = 3.97 ≒4.0(m)
答えは「a:4.0m」となります
まとめと余談
まとめとして、覚えるべき公式を再度記載しておきます
覚えるには数字を変えて反復練習するのがてっとり早いと思います
回転翼の消費パワー
P ∝ ρω3 ∝ Tω , W=T
r (旋回半径)についての式
r = V2 / g tanΦ
ある高度からの滑空距離
d = h / tanγ = h ・ ( L/D )
落下開始点から地上に墜落するまでの水平距離
x = v √( 2h / g )
フレネルゾーン半径の関係式
R = √{ λ × (D/4)} , λ = c / f
余談として公式を覚えたり使う際に、単位を意識するとわかりやすいかもしれません
今回程度の公式ではあまり気にしなくても大丈夫かと思いますが
左辺の求めたい値の単位と、右辺の計算式を計算した結果の単位は必ず一致します
例えば、車で走行する場合を想定して、距離を求めたいときには「速さ×時間」をすると思います
距離の単位はkm、速さはkm/h、時間はh
単位だけで式を表すと、「 km = km/h × h 」となります
右辺を計算すると、「 km/h × h 」となってkmだけが残り左辺と同じになります
もちろん「=」で結ばれているので当たり前の話ですが
つまり右辺はどんなに複雑な計算となっても、単位のヒントがあればある程度の公式は推測できるようになります
一等学科試験の計算問題は比較的簡単なので、得点源にしていくといいと思います
スポンサードリンク






コメント